백준 링크
https://www.acmicpc.net/problem/5719
5719번: 거의 최단 경로
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 장소의 수 N (2 ≤ N ≤ 500)과 도로의 수 M (1 ≤ M ≤ 104)가 주어진다. 장소는 0부터 N-1번까지 번호가 매겨져 있
www.acmicpc.net
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
| 1 초 | 256 MB | 25874 | 4649 | 2892 | 19.459% |
문제
요즘 많은 자동차에서는 GPS 네비게이션 장비가 설치되어 있다. 네비게이션은 사용자가 입력한 출발점과 도착점 사이의 최단 경로를 검색해 준다. 하지만, 교통 상황을 고려하지 않고 최단 경로를 검색하는 경우에는 극심한 교통 정체를 경험할 수 있다.
상근이는 오직 자기 자신만 사용 가능한 네비게이션을 만들고 있다. 이 네비게이션은 절대로 최단 경로를 찾아주지 않는다. 항상 거의 최단 경로를 찾아준다.
거의 최단 경로란 최단 경로에 포함되지 않는 도로로만 이루어진 경로 중 가장 짧은 것을 말한다.
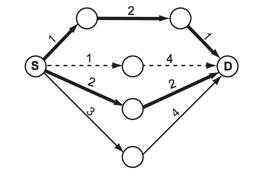
예를 들어, 도로 지도가 아래와 같을 때를 생각해보자. 원은 장소를 의미하고, 선은 단방향 도로를 나타낸다. 시작점은 S, 도착점은 D로 표시되어 있다. 굵은 선은 최단 경로를 나타낸다. (아래 그림에 최단 경로는 두 개가 있다)거의 최단 경로는 점선으로 표시된 경로이다. 이 경로는 최단 경로에 포함되지 않은 도로로 이루어진 경로 중 가장 짧은 경로이다. 거의 최단 경로는 여러 개 존재할 수도 있다. 예를 들어, 아래 그림의 길이가 3인 도로의 길이가 1이라면, 거의 최단 경로는 두 개가 된다. 또, 거의 최단 경로가 없는 경우도 있다.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 장소의 수 N (2 ≤ N ≤ 500)과 도로의 수 M (1 ≤ M ≤ 104)가 주어진다. 장소는 0부터 N-1번까지 번호가 매겨져 있다. 둘째 줄에는 시작점 S와 도착점 D가 주어진다. (S ≠ D; 0 ≤ S, D < N) 다음 M개 줄에는 도로의 정보 U, V, P가 주어진다. (U ≠ V ; 0 ≤ U, V < N; 1 ≤ P ≤ 103) 이 뜻은 U에서 V로 가는 도로의 길이가 P라는 뜻이다. U에서 V로 가는 도로는 최대 한 개이다. 또, U에서 V로 가는 도로와 V에서 U로 가는 도로는 다른 도로이다.
입력의 마지막 줄에는 0이 두 개 주어진다.
출력
각 테스트 케이스에 대해서, 거의 최단 경로의 길이를 출력한다. 만약, 거의 최단 경로가 없는 경우에는 -1을 출력한다.
예제 입력 1 복사
7 9
0 6
0 1 1
0 2 1
0 3 2
0 4 3
1 5 2
2 6 4
3 6 2
4 6 4
5 6 1
4 6
0 2
0 1 1
1 2 1
1 3 1
3 2 1
2 0 3
3 0 2
6 8
0 1
0 1 1
0 2 2
0 3 3
2 5 3
3 4 2
4 1 1
5 1 1
3 0 1
0 0
예제 출력 1 복사
5
-1
6코드 풀이
틀린 풀이
- 일반적인 다익스트라를 진행하는데 최단경로를 저장
- 저장된 경로를 못가는 경로라 지정(해당 경로의 Cost를 INF라 설정 = 다익스트라 풀이에서 continue로 넘어가도록 구현)
- RemoveTrace 진행 후 다시 다익스트라 진행
- 기존 최단경로와 같다면 다시 RemoveTrace 실행, 다르다면 거의 최단경로가 구해진것이므로 출력 후 종료
위와 같은 풀이로 코드를 작성했는데 시간 초과가 발생했다.
정답 풀이
우선 개인의 힘으로 풀지 못하여 다른 블로거의 포스팅을 참고하였습니다.
아래 출처 들어가보시면 정확한 설명 나와있습니다.!
실패 코드
#include <iostream>
#include <queue>
#include <algorithm>
#include <vector>
#include <string.h>
using namespace std;
#define INF 1000000000
#define MAX_NODE 501
int N, M;
int S, D;
vector<pair<int, int>> Graph[MAX_NODE];
int Dist[MAX_NODE];
int Route[MAX_NODE];
void Dijkstra(int StartNode)
{
fill(Dist, Dist + N, INF);
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({ 0, StartNode });
Dist[StartNode] = 0;
while (!pq.empty())
{
int CurNode = pq.top().second;
int CurCost = pq.top().first;
pq.pop();
if (Dist[CurNode] < CurCost)
continue;
int Size = static_cast<int>(Graph[CurNode].size());
for (int i = 0; i < Size; ++i)
{
if (Graph[CurNode][i].second == INF)
continue;
int NextNode = Graph[CurNode][i].first;
int NextCost = Graph[CurNode][i].second + CurCost;
if (Dist[NextNode] > NextCost)
{
pq.push({ NextCost, NextNode });
Dist[NextNode] = NextCost;
Route[NextNode] = CurNode;
}
}
}
}
void RemoveTrace(int StartNode, int EndNode)
{
Route[StartNode] = 0;
int Index = EndNode;
while (Route[Index] != 0)
{
for (size_t i = 0; i < Graph[Route[Index]].size(); ++i)
{
if (Graph[Route[Index]][i].first == Index)
{
Graph[Route[Index]][i].second = INF;
}
}
Index = Route[Index];
}
for (size_t i = 0; i < Graph[StartNode].size(); ++i)
{
if (Graph[StartNode][i].first == Index)
{
Graph[StartNode][i].second = INF;
break;
}
}
}
int main()
{
while (true)
{
cin >> N >> M;
if (N == 0 && M == 0)
break;
cin >> S >> D;
for (int i = 0; i < MAX_NODE; i++) {
Graph[i].clear(); // 벡터를 비워줌
}
int NodeA, NodeB, Cost;
for (int i = 0; i < M; ++i)
{
cin >> NodeA >> NodeB >> Cost;
Graph[NodeA].push_back({ NodeB, Cost });
}
int MinCost = INF;
int CurrentCost = INF;
while (MinCost == CurrentCost)
{
Dijkstra(S);
CurrentCost = Dist[D];
MinCost = min(MinCost, CurrentCost);
RemoveTrace(S, D);
}
if (INF != CurrentCost)
cout << CurrentCost << "\n";
else
cout << -1 << "\n";
}
return 0;
}정답 코드
#include <iostream>
#include <queue>
#include <algorithm>
#include <vector>
#include <string.h>
using namespace std;
#define INF 1000000000
#define MAX_NODE 501
int N, M;
int S, D;
vector<int> Graph[MAX_NODE];
vector<int> PrevNode[MAX_NODE];
int Dist[MAX_NODE];
int Route[MAX_NODE];
int V[MAX_NODE][MAX_NODE];
void Dijkstra(int StartNode)
{
fill(Dist, Dist + N, INF);
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({ 0, StartNode });
Dist[StartNode] = 0;
while (!pq.empty())
{
int CurNode = pq.top().second;
int CurCost = pq.top().first;
pq.pop();
if (Dist[CurNode] < CurCost)
continue;
int Size = static_cast<int>(Graph[CurNode].size());
for (int i = 0; i < Size; ++i)
{
int NextNode = Graph[CurNode][i];
int NextCost = V[CurNode][NextNode];
if (NextCost != 0 && Dist[NextNode] > NextCost + CurCost)
{
Dist[NextNode] = NextCost + CurCost;
PrevNode[NextNode].clear();
PrevNode[NextNode].push_back(CurNode);
pq.push({ Dist[NextNode], NextNode });
}
else if (NextCost != 0 && Dist[NextNode] == NextCost + CurCost)
{
PrevNode[NextNode].push_back(CurNode);
}
}
}
}
void RemoveTrace()
{
queue<int> q;
q.push(D);
bool Visited[MAX_NODE] = {};
Visited[D] = true;
while (!q.empty())
{
int Cur = q.front();
q.pop();
for (int i = 0; i < PrevNode[Cur].size(); ++i)
{
int Prev = PrevNode[Cur][i];
V[Prev][Cur] = 0;
if (!Visited[Prev])
{
q.push(Prev);
Visited[Prev] = true;
}
}
}
}
int main()
{
while (true)
{
cin >> N >> M;
if (N == 0 && M == 0)
break;
cin >> S >> D;
for (int i = 0; i < MAX_NODE; i++)
{
memset(V[i], 0, sizeof(int) * MAX_NODE);
Graph[i].clear(); // 벡터를 비워줌
PrevNode[i].clear();
}
int NodeA, NodeB, Cost;
for (int i = 0; i < M; ++i)
{
cin >> NodeA >> NodeB >> Cost;
Graph[NodeA].push_back(NodeB);
V[NodeA][NodeB] = Cost;
}
Dijkstra(S);
RemoveTrace();
Dijkstra(S);
if (Dist[D] == INF)
cout << -1 << '\n';
else
cout << Dist[D] << '\n';
}
return 0;
}정답 코드 출처
[백준 5719 C++] 거의 최단 경로
오늘은 백준 5719번 강의실 배정 문제에 대해 다뤄볼 예정이다. 강의실 배정 문제 링크 (백준 5719번 문제): https://www.acmicpc.net/problem/5719 5719번: 거의 최단 경로 입력은 여러 개의 테스트 케이스로 이
hackingis.art
'백준' 카테고리의 다른 글
| 백준 : 15688번 수 정렬하기5 (c++) (0) | 2023.09.18 |
|---|---|
| 백준 : 1158번 요세푸스 문제 (c++) (0) | 2023.09.15 |
| 백준 : 1854번 K번째 최단경로 찾기 다익스트라(c++) (0) | 2023.09.10 |
| 백준 : 1956번 운동 플로이드 와샬(c++) (0) | 2023.09.05 |
| 백준 : 14938번 서강그라운드 플로이드 와샬(c++) (0) | 2023.09.03 |


댓글