안녕하세요 틴구입니다.
안녕하세요 오늘은 자료구조 Graph에 관해서 설명을 해드리려고합니다.
1. Graph란
그래프는 정점과 간선으로 이루어진 자료구조입니다.
그래프를 구현하는 방법에는 인접행렬와 인접리스트방법이 있는데 저 같은 경우는
인접리스트방법으로 구현하도록 하겠습니다.
Graph에는 두가지의 종류가있는데
방향성 그래프와 무방향 그래프입니다(배운 가지수가 두가지)
방향성 그래프란 : 방향 그래프는 두 정점을 연결하는 간선에 방향이 존재하는 그래프입니다.
방향 그래프는 그 간선의 방향대로 움직일 수 있습니다.
Graph에는 탐색방법이 두가지의 종류가 있습니다
그래프 탐색의 방법은 깊이 우선 탐색(DFS) 방식과 너비 우선 탐색(BFS)방식이 있습니다.
깊이우선 탐색(DFS) : 갈 수 있는 정점까지 최대한 깊게 들어간다음 더이상 다음으로 갈 정점이 없다면 돌아와
다음 연결되어있는 정점으로 또 깊숙하게 들어가 탐색하는 구조입니다.(Stack활용)
너비우선 탐색(BFS) : 너비우선 탐색은 깊이우선 탐색과 다르게 처음 노드에서 인접한 정점들을 모두 방문 후 방문한 접점에서 인접한 접점들로 다시 방문하며 탐색하는 구조입니다.(Queue활용)Queue
2. Graph코드구성
우선 template 를 활용할거기 때문에 헤더파일에 클래스 - 인라인 으로 생성해줍니다.Graph헤더파일에 Edge와 GraphNode와 둘을 관리해주는 Graph class들을 만들어줍니다.

class CEdge 구성

class CGraphNode 구성
여기서 CEdge<T>** m_EdgeArray;로 설정한 이유는
노드를 연결하는 엣지가 몇개인지 알 수 없고 여러개가 있을 경우를 위해 포인터 배열로 선언을 한것이다.
bool m_Visit;는 노드에 방문했을 했는지 안 했는지 구분하기 위한 선언이다.

class CGraph 구성
여기서 class CGraph에다가 public:으로 void insert함수를 만들어줍니다
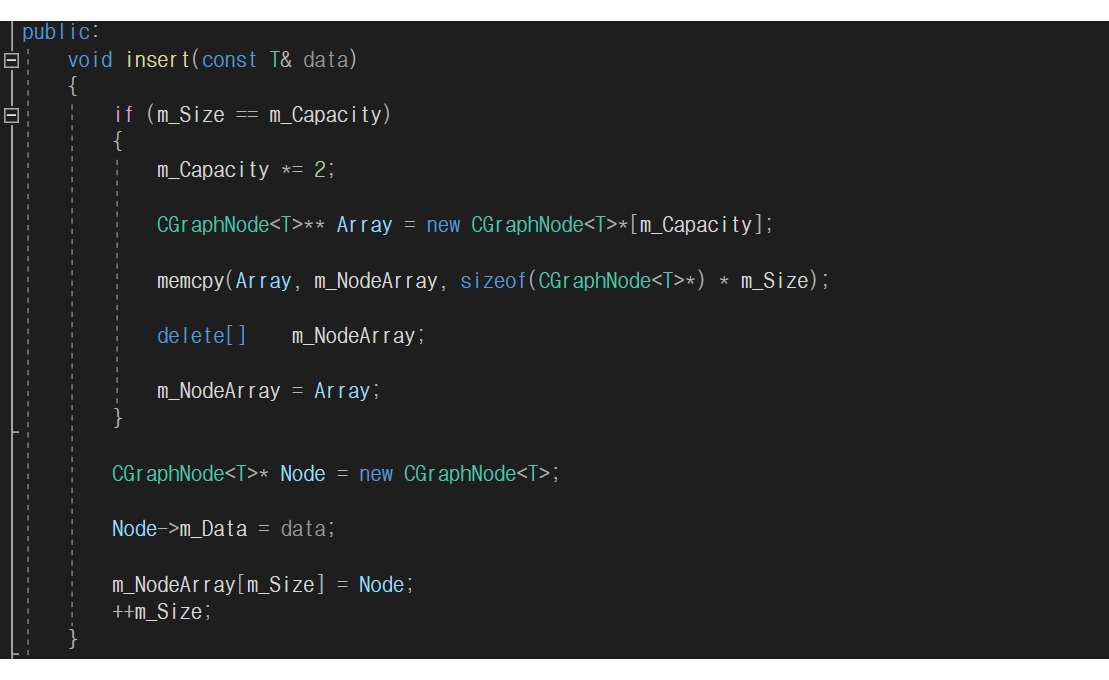
insert함수는 데이터의 값들을 넣어주는 함수입니다.
배열의 공간이 꽉찼을경우를 대비해서 자동으로 늘려주는 if문을 만들어줍니다.

다음으로는 CGraphNode에다가 private:로 void AddEdge함수를 만들어줍니다.
이 함수는 노드와 노드를 잇는 엣지를 만들어주는 함수입니다.
위 함수를 만든후

class CGraph에다가 void AddEdge(const T& Src, const T& Dest)함수를 만들어줍니다
위 함수는 노드와 노드 사이에 위에서 만든 엣지로 연결시키는 함수입니다.
여기까지가 기본 Graph코드 구성이고 다음으로는 탐색방법인
DFS, BFS코드 구성입니다
코드 보시기 전에 DFS의 경우는 Stack를 사용하고 BFS의 경우는 Queue을 활용하기 때문에
Queue와 Stack의 헤더파일을 갖고와줍니다.

BFS함수의 코드구성
m_Size가 0이라면 비어있다는 의미이므로 리턴으로 예외처리를 해줍니다.
시작하기 전에 모든 노드의 방문상태를 false로 만들어줍니다.
상단에 #include "Queue.h"을 불러와
Queue를 사용하기위해 코드를 구성합니다.
시작지점인 m_NodeArray[0]을 알 수 있게 queue.push함수의 인자에 넣어주고
push를 했다는것은 방문을 했다는 것이기 때문에 m_Visit을 true로 바꿔준다.
while문에 들어가서 조건에 성립하면
첫 시작점인 front값을 큐에 얻어오고 팝을한 뒤
노드가 가지고있는 엣지를 이용해서 Add(queue)를 넣어서(엣지에 메달려있는 노드들을 queue에 넣는것)
인자로 들어온 펑션을 이용해서 노드의 값을 출력하는 방법입니다.
Add()함수는 아래 참고

queue를 인자로 넣으면 BFS

stack을 인자로 넣으면 DFS

DFS도 BFS랑 동일한 코드구성이다 중간에 queue를 stack으로만 바꿔주면 된다
'c++ > 자료구조' 카테고리의 다른 글
| 20210811 Hashtable (0) | 2021.08.12 |
|---|---|
| 20210810 Dijkstra(다익스트라) 알고리즘 (0) | 2021.08.11 |
| 20210810 병합정렬(합병정렬) (0) | 2021.08.10 |
| 20210806 Heap정렬, Quick정렬 (0) | 2021.08.08 |
| 20210805 자가균형 이진트리 AVLTree (0) | 2021.08.06 |


댓글