프로그래머스 링크
https://school.programmers.co.kr/learn/courses/30/lessons/43105
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명
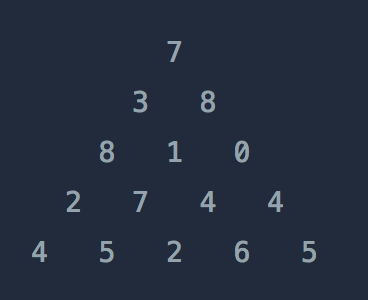
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.
제한사항- 삼각형의 높이는 1 이상 500 이하입니다.
- 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.
| [[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] | 3 |
풀이
위 문제 설명에서 가장 중요하게 생각해야되는 부분은
아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
부분같다.
0
1 2
3 4 5
6 7 8 9
의 삼각형이 있다고 생각해보자
이때 가장 왼쪽 원소는 각 배열의 0번 인덱스 값이 된다
그러면 가장 오른쪽 원소는??
i x j 인덱스의 원소가 되게된다
(가로 세로 한개씩 늘어나기 때문에)
그럼 7번 원소를 구하기 위해서는
(3 + 7) 1번 (4 + 7) 1번 총 두번의 계산이 필요하게 된다
즉 i가 세로 j가 가로 인덱스를 뜻한다고 하면
[i - 1][j - 1]과 [i - 1][j] 두개를 비교하여 큰 값을 찾으면 된다.
코드
#include <string>
#include <vector>
#include <cmath>
using namespace std;
// 최대값 저장할 공간
int SaveArray[501][501];
int solution(vector<vector<int>> triangle) {
int answer = 0;
// 맨 꼭대기는 바로 저장
SaveArray[0][0] = triangle[0][0];
int Size = triangle.size();
// 나머지는 반복문 돌면서 저장
for(int i = 1; i < Size; ++i)
{
for(int j = 0; j <= i; ++j)
{
// j가 0 즉 가로가 0번인덱스라면 제일 왼쪽 원소라는것
if(j == 0)
{
SaveArray[i][j] = SaveArray[i - 1][j] + triangle[i][j];
}
// i랑 j가 같다면 제일 오른쪽 원소라는거
else if(i == j)
{
SaveArray[i][j] = SaveArray[i - 1][j - 1] + triangle[i][j];
}
// 위에 둘다 아니라면 중앙 원소들이라는것
else
{
// 중앙 원소는 i - 1 위에 원소 두개랑 비교를 해야됨
SaveArray[i][j] = max(SaveArray[i - 1][j - 1] + triangle[i][j], SaveArray[i - 1][j] + triangle[i][j]);
}
answer = max(answer, SaveArray[i][j]);
}
}
return answer;
}정확성

'프로그래머스 > lv3' 카테고리의 다른 글
| 프로그래머스 : 연습문제 > 야근 지수(lv3) c++ (0) | 2023.04.19 |
|---|---|
| 프로그래머스 : 깊이/너비 우선 탐색(DFS/BFS) > 단어 변환(lv3) c++ (0) | 2023.04.18 |
| 프로그래머스 : 깊이/너비 우선 탐색(DFS/BFS) > 아이템 줍기(lv3) (0) | 2023.04.07 |
| 프로그래머스 : 깊이/너비 우선 탐색(DFS/BFS) > 네트워크(lv3) (0) | 2023.04.06 |
| 프로그래머스 : 최고의 집합(lv3) (0) | 2023.04.02 |


댓글