프로그래머스 링크
https://school.programmers.co.kr/learn/courses/30/lessons/67259
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명

건설회사의 설계사인 죠르디는 고객사로부터 자동차 경주로 건설에 필요한 견적을 의뢰받았습니다.
제공된 경주로 설계 도면에 따르면 경주로 부지는 N x N 크기의 정사각형 격자 형태이며 각 격자는 1 x 1 크기입니다.
설계 도면에는 각 격자의 칸은 0 또는 1 로 채워져 있으며, 0은 칸이 비어 있음을 1은 해당 칸이 벽으로 채워져 있음을 나타냅니다.
경주로의 출발점은 (0, 0) 칸(좌측 상단)이며, 도착점은 (N-1, N-1) 칸(우측 하단)입니다. 죠르디는 출발점인 (0, 0) 칸에서 출발한 자동차가 도착점인 (N-1, N-1) 칸까지 무사히 도달할 수 있게 중간에 끊기지 않도록 경주로를 건설해야 합니다.
경주로는 상, 하, 좌, 우로 인접한 두 빈 칸을 연결하여 건설할 수 있으며, 벽이 있는 칸에는 경주로를 건설할 수 없습니다.
이때, 인접한 두 빈 칸을 상하 또는 좌우로 연결한 경주로를 직선 도로 라고 합니다.
또한 두 직선 도로가 서로 직각으로 만나는 지점을 코너 라고 부릅니다.
건설 비용을 계산해 보니 직선 도로 하나를 만들 때는 100원이 소요되며, 코너를 하나 만들 때는 500원이 추가로 듭니다.
죠르디는 견적서 작성을 위해 경주로를 건설하는 데 필요한 최소 비용을 계산해야 합니다.
예를 들어, 아래 그림은 직선 도로 6개와 코너 4개로 구성된 임의의 경주로 예시이며, 건설 비용은 6 x 100 + 4 x 500 = 2600원 입니다.
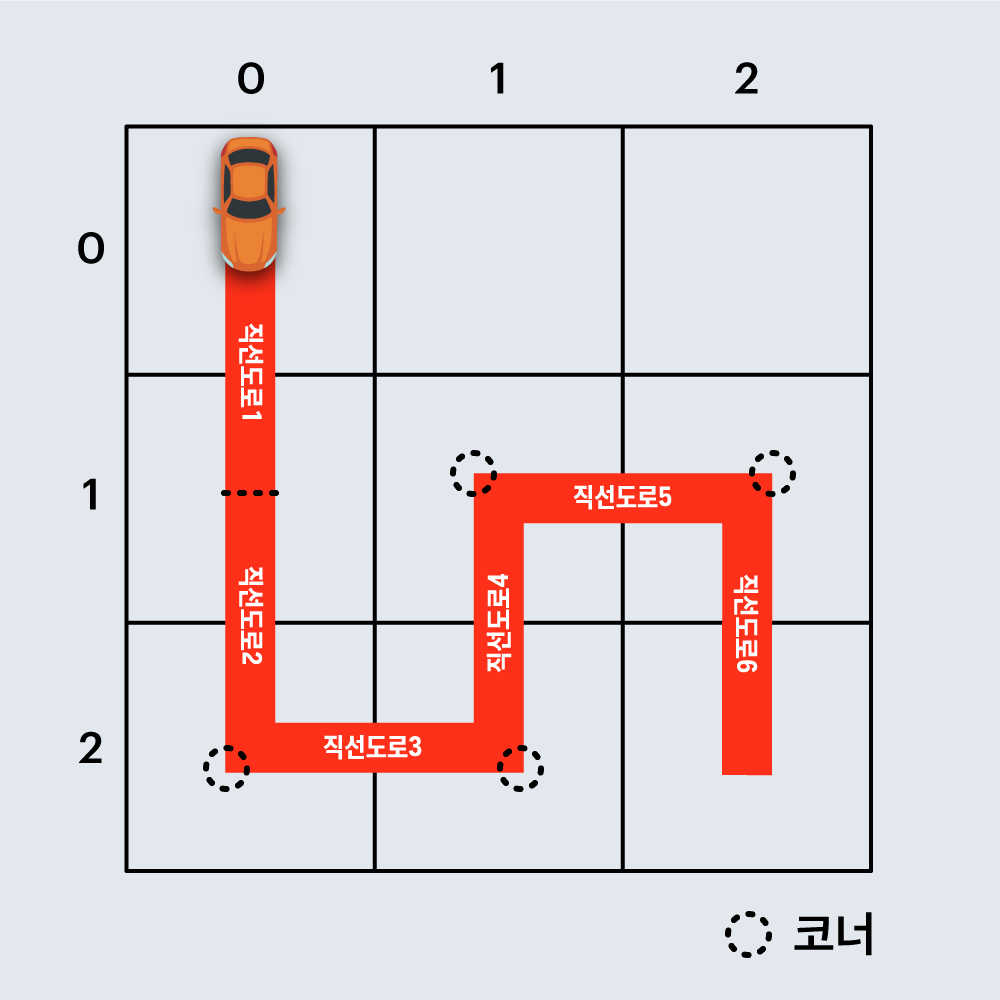
또 다른 예로, 아래 그림은 직선 도로 4개와 코너 1개로 구성된 경주로이며, 건설 비용은 4 x 100 + 1 x 500 = 900원 입니다.
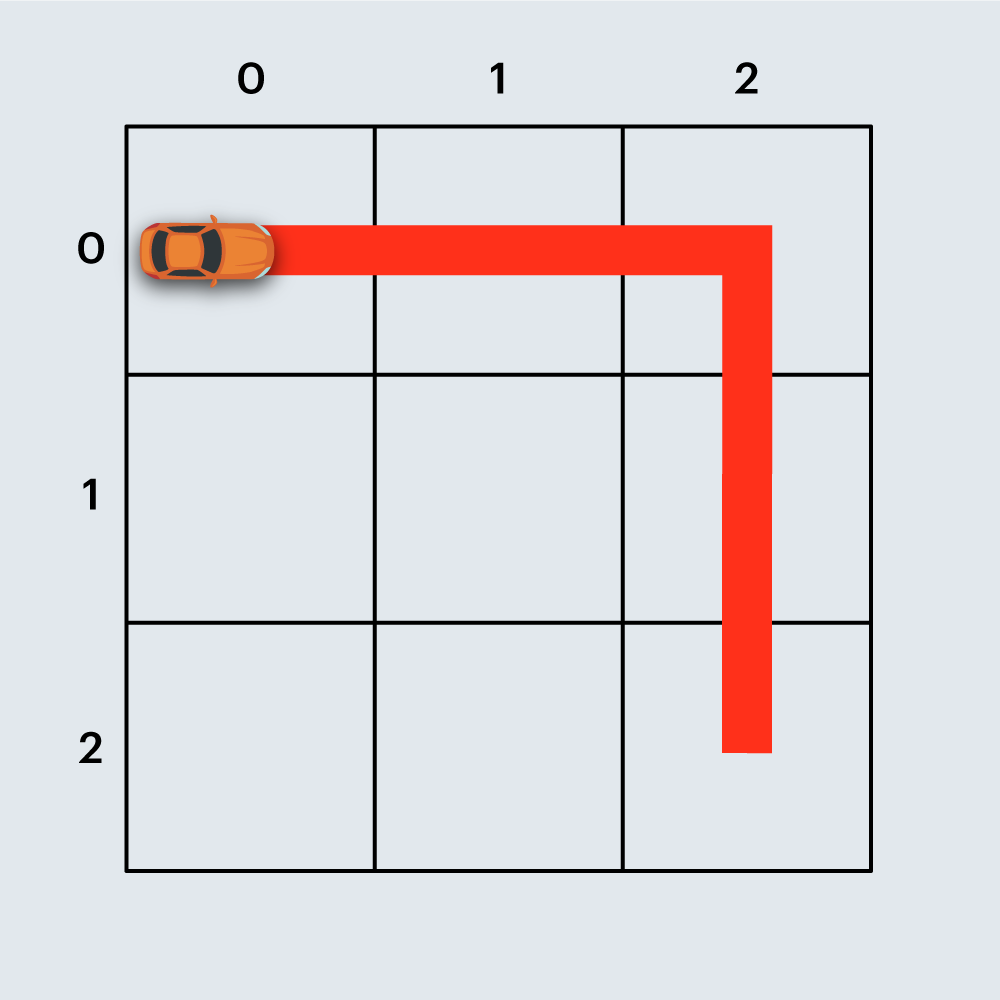
도면의 상태(0은 비어 있음, 1은 벽)을 나타내는 2차원 배열 board가 매개변수로 주어질 때, 경주로를 건설하는데 필요한 최소 비용을 return 하도록 solution 함수를 완성해주세요.
[제한사항]- board는 2차원 정사각 배열로 배열의 크기는 3 이상 25 이하입니다.
- board 배열의 각 원소의 값은 0 또는 1 입니다.
- 도면의 가장 왼쪽 상단 좌표는 (0, 0)이며, 가장 우측 하단 좌표는 (N-1, N-1) 입니다.
- 원소의 값 0은 칸이 비어 있어 도로 연결이 가능함을 1은 칸이 벽으로 채워져 있어 도로 연결이 불가능함을 나타냅니다.
- board는 항상 출발점에서 도착점까지 경주로를 건설할 수 있는 형태로 주어집니다.
- 출발점과 도착점 칸의 원소의 값은 항상 0으로 주어집니다.
입출력 예 | board | result
| [[0,0,0],[0,0,0],[0,0,0]] | 900 |
| [[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0],[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0],[0,0,0,1,0,0,0,1],[0,0,1,0,0,0,1,0],[0,1,0,0,0,1,0,0],[1,0,0,0,0,0,0,0]] | 3800 |
| [[0,0,1,0],[0,0,0,0],[0,1,0,1],[1,0,0,0]] | 2100 |
| [[0,0,0,0,0,0],[0,1,1,1,1,0],[0,0,1,0,0,0],[1,0,0,1,0,1],[0,1,0,0,0,1],[0,0,0,0,0,0]] | 3200 |
코드 풀이
이번 문제는 BFS 방식으로 구현하였습니다.
위 문제에서 주의해야 할 점은 직선도로와 코너를 건설할 때의 가격이 다르다는 점이고 도착지점까지 건설비용을 최소화하는 점을 주의해서 봐야 합니다.
풀이 방식 큰 틀
- Cost의 모든 값을 INT_MAX값으로 설정(최솟값을 구해야 하기 때문)
- 큐가 빌 때까지 BFS 탐색
- 현재 노드의 값을 빼놓고 4방향 탐색
- 다음 노드가 코너인지 아닌지 판단 후 다음 노드의 Cost값 구해준다
- 다음 노드의 기존 가격이 새로 구한 가격보다 작다면 Cost값 갱신 후 queue.push(Next)
- 모든 BFS 탐색이 끝났다면 최종 위치의 4방향 중 가장 작은 값 리턴
헷갈리면 안 되는 부분
- 코너지점의 가격은 직선 + 코너가격이 되어야 한다.
- 첫 시작지점을 직선도로로 포함하면 안 된다.
- 도착지점까지의 최소 건설 비용을 구해야 하기 때문에 재방문이 가능해야 된다.
저도 위 3가지 때문에 엄청 헷갈렸던 문제였습니다...
코드
#include <string>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
#define INT_MAX 2147483647
int Cost[26][26][4];
int dx[4] = { 1, 0, -1, 0 };
int dy[4] = { 0, 1, 0, -1 };
struct Data
{
int X;
int Y;
int Dir;
};
int solution(vector<vector<int>> board) {
int answer = 0;
queue<Data> qPos;
//queue<pair<int, int>> qPrevPos;
qPos.push({ 0, 0, -1 });
int BoardSize = board.size();
for (int i = 0; i < BoardSize; ++i)
{
for (int j = 0; j < BoardSize; ++j)
{
for (int k = 0; k < 4; ++k)
{
Cost[i][j][k] = INT_MAX;
}
}
}
for (int i = 0; i < 4; ++i)
{
Cost[0][0][i] = 0;
}
// 첫 시작지점은 무조건 직진
Cost[0][0][0] = 100;
while (!qPos.empty())
{
Data Cur = qPos.front();
qPos.pop();
for (int Dir = 0; Dir < 4; ++Dir)
{
Data Next;
Next.X = Cur.X + dx[Dir];
Next.Y = Cur.Y + dy[Dir];
Next.Dir = Dir;
int NextCost = Cost[Cur.Y][Cur.X][Cur.Dir];
if (Next.X < 0 || Next.Y < 0
|| Next.X >= BoardSize || Next.Y >= BoardSize
|| board[Next.Y][Next.X] == 1)
continue;
NextCost += 100;
// 현재의 방향이 왼쪽, 오른쪽이고
if (Cur.Dir == 0 || Cur.Dir == 2)
{
// 다음 방향이 위, 아래라면 코너이다.
if (Next.Dir == 1 || Next.Dir == 3)
{
NextCost += 500;
}
}
// 현재의 방향이 위, 아래거나
else if (Cur.Dir == 1 || Cur.Dir == 3)
{
// 다음 방향이 왼, 오른쪽 중 하나라면 코너
if (Next.Dir == 0 || Next.Dir == 2)
{
NextCost += 500;
}
}
// 다음 위치 새로 측정한 가격이 기존 가격보다 작다면 갱신
if (NextCost < Cost[Next.Y][Next.X][Next.Dir])
{
Cost[Next.Y][Next.X][Next.Dir] = NextCost;
qPos.push(Next);
}
}
}
// 최종 가격 최소값
answer = *min_element(Cost[BoardSize - 1][BoardSize - 1], Cost[BoardSize - 1][BoardSize - 1] + 4);
return answer;
}'프로그래머스 > lv3' 카테고리의 다른 글
| 프로그래머스 : 월간 코드 챌린지 시즌2 > 모두 0으로 만들기(lv3) c++ (5) | 2023.08.04 |
|---|---|
| 프로그래머스 : 2019 카카오 개발자 겨울 인턴십 > 불량 사용자(lv3) c++ (0) | 2023.06.29 |
| 프로그래머스 : 2020 카카오 인턴십 > 보석 쇼핑(lv3) c++ (0) | 2023.06.28 |
| 프로그래머스 : Summer/Winter Coding(~2018) > 기지국 설치(lv3) c++ (0) | 2023.06.05 |
| 프로그래머스 : Summer/Winter Coding(~2018) > 숫자 게임(lv3) c++ (0) | 2023.05.31 |


댓글