프로그래머스 링크
https://school.programmers.co.kr/learn/courses/30/lessons/12978
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명
N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.
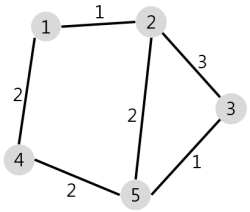
위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.
- 마을의 개수 N은 1 이상 50 이하의 자연수입니다.
- road의 길이(도로 정보의 개수)는 1 이상 2,000 이하입니다.
- road의 각 원소는 마을을 연결하고 있는 각 도로의 정보를 나타냅니다.
- road는 길이가 3인 배열이며, 순서대로 (a, b, c)를 나타냅니다.
- a, b(1 ≤ a, b ≤ N, a != b)는 도로가 연결하는 두 마을의 번호이며, c(1 ≤ c ≤ 10,000, c는 자연수)는 도로를 지나는데 걸리는 시간입니다.
- 두 마을 a, b를 연결하는 도로는 여러 개가 있을 수 있습니다.
- 한 도로의 정보가 여러 번 중복해서 주어지지 않습니다.
- K는 음식 배달이 가능한 시간을 나타내며, 1 이상 500,000 이하입니다.
- 임의의 두 마을간에 항상 이동 가능한 경로가 존재합니다.
- 1번 마을에 있는 음식점이 K 이하의 시간에 배달이 가능한 마을의 개수를 return 하면 됩니다.
입출력 예 | N | road | K | result
| 5 | [[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]] | 3 | 4 |
| 6 | [[1,2,1],[1,3,2],[2,3,2],[3,4,3],[3,5,2],[3,5,3],[5,6,1]] | 4 | 4 |
입출력 예 #1
문제의 예시와 같습니다.
입출력 예 #2
주어진 마을과 도로의 모양은 아래 그림과 같습니다.

1번 마을에서 배달에 4시간 이하가 걸리는 마을은 [1, 2, 3, 5] 4개이므로 4를 return 합니다.
코드 풀이
다익스트라 알고리즘을 이용하여 풀이 하였습니다.
1. 문제를 풀기위한 변수 생성(Graph, Cost 등등)
2. 각 노드를 Graph배열에 연결
3. 다익스트라의 경우 최소 거리를 판단하는 알고리즘이기 때문에 Cost를 임의의 숫자 Max치로 초기화
4. 다익스트라 알고리즘 수행
4.a 우선순위 큐와 std::greater를 이용하여 최소 비용의 노드부터 탐색
4.b 현재 노드의 비용이 k보다 크다면 다음 노드도 k의 비용보다 크다는 의미이므로 예외처리
4.c 다음 노드의 비용을 현재노드의 비용과 가중치를 더해두어 최소값으로 갱신해준다.
5. 알고리즘 종료 후 정답을 구한다.
코드
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
#define INF 1e9 // 무한을 의미하는 값으로 10억을 설정
vector<pair<int, int>> Graph[51]; // 그래프
int Cost[51]; // 노드별 최종 Cost값 저장할 배열
int answer = 0; // 정답
void Dijkstra(int Start, int k)
{
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pQueue;
pQueue.push({ 0, Start });
Cost[Start] = 0;
while (!pQueue.empty())
{
int CurNode = pQueue.top().second;
int CurCost = pQueue.top().first;
pQueue.pop();
// 현재 노드의 비용아 k보다 크다면 다음 노드도 k보다 크다는 의미이므로 continue;
if(CurCost > k)
continue;
for (int i = 0; i < Graph[CurNode].size(); ++i)
{
int NextNode = Graph[CurNode][i].first;
int NextCost = Graph[CurNode][i].second;
if (Cost[CurNode] + NextCost < Cost[NextNode])
{
Cost[NextNode] = Cost[CurNode] + NextCost;
pQueue.push({Cost[NextNode], NextNode});
}
}
}
}
int solution(int N, vector<vector<int> > road, int K) {
int Size = static_cast<int>(road.size());
// 그래프 연결
for (int i = 0; i < Size; ++i)
{
Graph[road[i][0]].push_back({ road[i][1], road[i][2] });
Graph[road[i][1]].push_back({ road[i][0], road[i][2] });
}
// 최소값을 구해야 하기 때문에 최대값으로 임의 초기화
fill(Cost, Cost + 51, INF);
// 다익스트라 알고리즘 시작 1번 노드부터 시작
Dijkstra(1, K);
// 마지막에 최종 정답을 구해야 함
// 알고리즘 노드별 계산할때마다 판단하여 구하게 되면
// 입출력 예 3 -> 5 갈때 처럼 간선이 2개가 있고 3노드의 Cost + 두 개의 가중치 값이 전부 K
// 보다 작다면 answer이 2번 증가하게 된다
// 이러한 부분때문에 answer은 마지막에 구해주었다.
for(int i = 0; i <= N; ++i)
{
if(Cost[i] <= K)
++answer;
}
return answer;
}'프로그래머스 > lv2' 카테고리의 다른 글
| 프로그래머스 : 연습문제 > 연속 부분 수열 합의 개수(lv2 (0) | 2023.07.28 |
|---|---|
| 프로그래머스 : 연습문제 > 택배상자(lv2) c++ (0) | 2023.06.27 |
| 프로그래머스 : 연습문제 > 무인도 여행(lv2) c++ BFS풀이 (2) | 2023.06.11 |
| 프로그래머스 : 연습문제 > 뒤에 있는 큰 수 찾기(lv2) c++ (0) | 2023.06.04 |
| 프로그래머스 : Summer/Winter Coding(~2018) > 스킬트리(lv2) c++ (0) | 2023.06.03 |


댓글