프로그래머스 : 탐욕법(Greedy) > 섬 연결하기(lv3) c++

프로그래머스 링크

https://school.programmers.co.kr/learn/courses/30/lessons/42861#

프로그래머스

문제 설명

n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.

다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.

제한사항

• 섬의 개수 n은 1 이상 100 이하입니다.
• costs의 길이는 ((n-1) * n) / 2이하입니다.
• 임의의 i에 대해, costs[i][0] 와 costs[i] [1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i] [2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
• 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
• 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
• 연결할 수 없는 섬은 주어지지 않습니다.

입출력 예

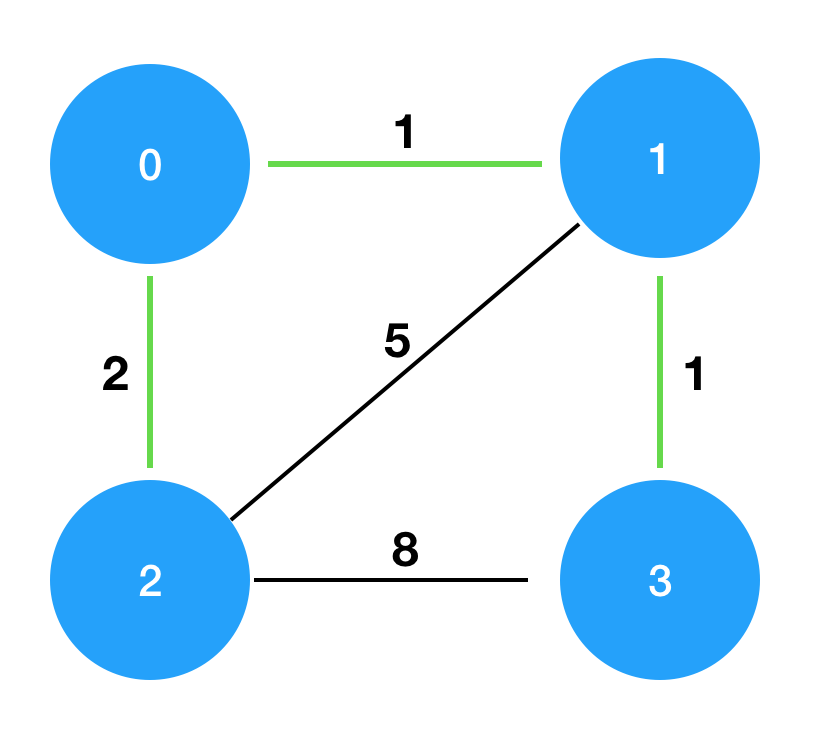
n | costs | return

4

[[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]]

4

입출력 예 설명

costs를 그림으로 표현하면 다음과 같으며, 이때 초록색 경로로 연결하는 것이 가장 적은 비용으로 모두를 통행할 수 있도록 만드는 방법입니다.

코드 풀이

처음 이미지를 보고 떠오른 방법은 다익스트라의 방법을 응용하는거였다

하지만 다익스트라의 경우 시작점에서 도착점의 간선의 최소값을 구하는 알고리즘이라 조금의 수정이 필요했다.

기존의 다익스트라는 가중치값을 더해가며 판단하는 방식인데 이 부분을 더한값이 아닌 다음 노드까지의 가중치값이랑 비교를 해주었다.

 

그리고 다른 분들의 풀이를 보니깐 다익스트라 방식 말고 크루스칼 알고리즘을 사용한 방식도 보여 살펴보았다.

크루스칼 방식은 가중치값을 오름차순이 되게끔 벡터를 정렬시킨뒤

가장 작은 가중치값을 갖고있는 섬 부터 차례대로 연결해준다.

이때 중요한 부분은 연결을 시키기전 노드들이 하나의 써클이 되지 않는다면 두 노드를 연결시킨다

즉 두 노드의 부모노드가 다르다면 연결이 가능한것.

 

코드(다익스트라 알고리즘)

#include <string>
#include <vector>
#include <algorithm>
#include <queue>

using namespace std;
#define INF 1e9 // 무한을 의미하는 값으로 10억을 설정

vector<pair<int, int> > graph[101]; 
int d[101]; 
bool Visit[101];

void dijkstra(int start)
{
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq; // 거리, 노드 인덱스 + 정렬

    pq.push({ 0,start }); //시작 노드로 가기위한 최단 경로는 0으로 설정하여, 큐에 삽입.
    d[start] = 0;

    while (!pq.empty())
    {
        int dist = pq.top().first; //현재 노드까지의 비용
        int now = pq.top().second; // 현재 노드
        pq.pop();

        // 이번노드는 방문했으니 true
        Visit[now] = true;

        for (int i = 0; i < graph[now].size(); i++)
        {
            int cost = graph[now][i].second; // 거쳐서 가는 노드의 비용을 계산

            int Next = graph[now][i].first; // 다음 노드

            // 방문이 안된노드이고 비용이 작다면
            if (!Visit[Next] && cost < d[graph[now][i].first]) 
            {
                d[graph[now][i].first] = cost;
                pq.push(make_pair(cost, graph[now][i].first));
            }
        }
    }
}

int solution(int n, vector<vector<int>> costs) {
    int answer = 0;
    
    sort(costs.begin(), costs.end());

    // 모든 간선 정보를 입력받기
    for (int i = 0; i < costs.size(); i++)
    {
        // a번 노드에서 b번 노드로 가는 비용이 c라는 의미
        graph[costs[i][0]].push_back({ costs[i][1], costs[i][2] });
        graph[costs[i][1]].push_back({ costs[i][0], costs[i][2] });
    }

    // 최단 거리 테이블을 모두 무한으로 초기화
    fill(d, d + 101, INF);

    // 다익스트라 알고리즘을 수행
    dijkstra(costs[0][0]);

    // 모든 노드로 가기 위한 최단 거리를 출력
    for (int i = 0; i < n; i++)
    {
        answer += d[i];
    }
    
    return answer;
}

 

코드(크루스칼 알고리즘)

#include <string>
#include <vector>
#include <algorithm>

using namespace std;

vector<int> Node(101, -1);

int GetParent(int _node) 
{
    if (Node[_node] == _node) 
        return _node;
    
    return GetParent(Node[_node]);
}

bool SortFunc(const vector<int>& a, const vector<int>& b) 
{
    return a[2] < b[2];
}

int solution(int n, vector<vector<int>> costs) {
    int answer = 0;
    
    // costs의 2번 인덱스의 비용에 따른 오름차순 정렬
    sort(costs.begin(), costs.end(), SortFunc);

    for (int i = 0; i < n; i++)
    {
        Node[i] = i;
    }

    int CostsSize = costs.size();
    
    for (int i = 0; i < CostsSize; i++) 
    {
        int start = GetParent(costs[i][0]);
        int end = GetParent(costs[i][1]);
        int cost = costs[i][2];

        if (start != end) 
        {  
            // cycle이 만들어지지 않을 경우 다리를 추가
            answer += cost;
            Node[end] = start;
        }
    }
    
    return answer;
}

---

두알고리즘은 많이 접해보지 않은 알고리즘이라 많이 공부해야겠다